Akkordskala
Akkordskala-app
<alert type=«success» icon=«glyphicon glyphicon-user» dismiss=«true»> Kan åpnes i eget vindu | Se eksempler på grep nedenfor for de vanligste durtoneartene.</alert>
En akkordskala består av de akkorder du kan hente ut av en gitt skala. Dur- og mollskalaer har syv skalatrinn. Det gir da en akkordskala på syv akkorder.
Eksempel: F-dur har følgende skalatoner: f, g, a, bb, c, d og e:
<imgcaption skala1| F-durskalaen, med skalatrinn angitt med romertall>
 </imgcaption>
</imgcaption>
Akkordene bygges med tre eller flere toner fra skalaen, og annenhver skalatone oppover. Det kalles gjerne ters-stabler - det er et intervallet på en ters - mellom annenhver tone i skalaen.
For treklanger får vi da følgende akkorder i F-dur:
<imgcaption skala2| F-durskalaen harmonisert med treklanger>
 </imgcaption>
</imgcaption>
Hvordan skal vi så besifre akkordene?
Vi kan gjøre det ved å finne ut om intervallene mellom akkordtonene er små eller store terser.
Hvis den første tersen er liten, så blir akkorden en mollakkord. Hvis den først og den andre er en liten ters får vi en forminsket treklang (dim).
En annen måte å besifre er å ta utgangspunkt i det forhold at vi vet hva slags akkorder vi alltid får på hvert skalatrinn.
I dur vil første, fjerde og femte trinn alltid være en durakkord. Andre, tredje og sjette trinn vil alltid være en mollakkorder. Og syvende trinn vil det være en mollaakkord med liten kvint (b5), være seg en forminsket akkord (VIIdim) for treklanger, VIIm7b5 for fireklanger, VIIm9b5 for femklanger.
| Skalatrinn | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| akkordtype | durakkord | mollakkord | mollakkord | durakkord | durakkord | mollakkord | dim (forminsket treklang) |
| treklanger i F-dur | F | Gm | Am | Bb | C | Dm | Edim |
De besifrede treklangene i F-dur ser da slik ut:
<imgcaption skala3| Besifring av F-durskalaen harmonisert treklanger>
 </imgcaption>
</imgcaption>
Med gitargrep kan treklangene i F-dur da for eksempel se slik ut:
<imgcaption skala4| F-durskalaen harmonisert med treklanger. Gitargrep>
 </imgcaption>
</imgcaption>
Her er en tabell som viser mer i detalj hvordan akkorder bygges fra durskalaen.
| F-durskalaen | F | G | A | Bb | C | D | E | F | G | A | Bb | C | D | Harmonisk funksjon |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | F | A | C | I | ||||||||||
| Gm | G | Bb | D | ii | ||||||||||
| Am | A | C | E | iii | ||||||||||
| Bb | Bb | D | F | IV | ||||||||||
| C | C | E | G | V | ||||||||||
| Dm | D | F | A | Vi | ||||||||||
| Edim | E | G | Bb | Vii | ||||||||||
| F | F | A | C | I | ||||||||||
| Gm | G | Bb | D | ii | ||||||||||
| Intervaller | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 |
Legg merke til at hver andre akkord i akkordskalaen har to felles akkordtoner (mer om det nedenfor).
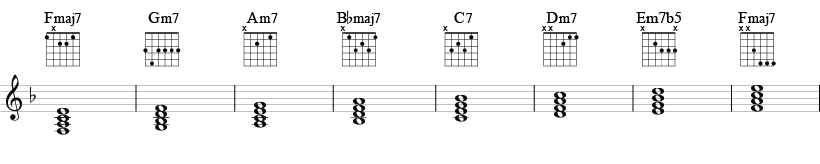
F-durskalaen harmonisert med fireklanger. Her får vi stor septim (besifres «maj7») på første og fjerde skalatrinn, og ellers liten septim (b7, besifres med «7»).
<imgcaption skala5| F-durskalaen harmonisert med fireklanger. Gitargrep>
 </imgcaption>
</imgcaption>
| F-durskalaen | F | G | A | Bb | C | D | E | F | G | A | Bb | C | D | E | F | Harmonisk funksjon |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fmaj7 | F | A | C | E | I | |||||||||||
| Gm7 | G | Bb | D | F | ii | |||||||||||
| Am7 | A | C | E | G | iii | |||||||||||
| Bbmaj7 | Bb | D | F | A | IV | |||||||||||
| C7 | C | E | G | Bb | V | |||||||||||
| Dm7 | D | F | A | C | Vi | |||||||||||
| Em7b5 | E | G | Bb | D | Vii | |||||||||||
| Fmaj7 | F | A | C | E | I | |||||||||||
| Gm7 | G | Bb | D | F | ii | |||||||||||
| Intervaller | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 |
Hvordan husker du hvilke toner som inngår i en akkord. En ting er å huske at det er annenhver tone i skalaen.
En annen teknikk er å lage melodiske sekvenser fra skalaen og synge dem til de sitter. Nyttig for øret: C-E-G-G-E-C D-F-A-A-F-D E-G-B-B-E-G G-H-D-D-H-G A-C-E-E-C-A B-D-F-F-D-B
Felles toner i annenhver akkord
Fellestoner (i to akkorder i en akkordprogresjon) kan betraktes som toner som forbinder den ene akkorden med den andre.
Studer tabellen over ser du at treklanger i ters-avstand har to toner felles, enten du går en ters ned eller opp. Sagt med andre ord: annenhver treklang i en akkordskala har to felles toner. Det samme prinsippet om fellestoner gjelder for to fireklang i ters-avstand. De har tre toner felles.
Eksempel: Hvis du harmoniserer f-durskalaen med treklanger, får du akkordene F-Gm-Am-Hb-C-Dm-Edim-F. Ok. La os da føre inn annenhver akkord i F-dur oppover gitarhalsen.
I iii V vii ii
|<--F-->| |<--Am->| |<--C-->| |<---Edim-->| |<--Gm->|
| | | | | | | | | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|-C-|---|---|---|-E-|---|---|-G-|---|---|-Bb|---|---|---|-D-|---|---|---|
|---|-A-|---|---|-C-|---|---|---|-E-|---|---|-G-|---|---|-Bb|---|---|---|
|---|---|-F-|---|---|---|-A-|---|---|-C-|---|---|---|-E-|---|---|-G-|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 5 | 7 9 | 12 | 15 | 17
| | | | |
|<------------->|<--------->|<------------->|<--------->|
stor ters liten ter stor ters liten ters
Hvis du går fra F til Am, finner du at de har tonene A og C felles. Tonen F er unik for F-en, mens E er unik for Am. Hvis du går fra Am til C, så finner du at de har tonene C og E til felles, mens A er unik for Am, mens G er unik for C.
Så er spørsmålet hvor blir det av den unike tonen fra en til en annen akkord?
Ta overgangen mellom C-A-F til A-C-E. Legg merke til at tonen F befinner seg ett bånd fra E.
<----F----> <----Am--->
|---|---|---|---|---|---|---|
|-C-|---|---|---|-E-|---|---|
|---|-A-|---|---|-C-|---|---|
|---|---|-F-|---|---|---|-A-|
|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|
3 5 7
Det betyr at du enkelt kan gjøre om en F til en Am og omvendt, ved bare å flytte tonen E ett bånd ned eller opp.
<----Am---> <----F---->
|---|---|---|---|---|---|---|
|-C-|---|---|---|---|-F-|---|
|---|-A-|---|---|-C-|---|---|
|---|-E-|---|---|---|---|-A-|
|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|
3 5 7
Du vil finne at den overskytende tonen altid befinner seg ett eller to bånd unna den unike tonen i hver av akkordene.
Inversjoner av akkorder fra akkordskala
Ved å flytte bare en tone fra annenhver akkord i en akkordskala, så finner du akkordenes inversjoner
<----Am----> <----Am---->
|---|---|---|---|---|---|---|
|-C-|---|---|---|-E-|---|---|
|---|-A-|---|---|-C-|---|---|
|---|-E-|---|---|---|---|-A-|
|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|
3 5 7
<----F----> <----F---->
|---|---|---|---|---|---|---|
|-C-|---|---|---|---|-F-|---|
|---|-A-|---|---|-C-|---|---|
|---|---|-F-|---|---|---|-A-|
|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|
3 5 7
En treklang har tre toner og dermed tre inversjoner. Du kan finne alle inversjonene av tonene på samme måte som over.
Vi ser at I-akkorden F og V-akkorden C har en tone felles, nemlig C. Så for å forandre en V-akkorden til en inversjon av en I-akkord, trenger vi å flytte på to toner. Vi har allerede gjort om iii-akkorden til en I-akkord ved å flyttet på en enkelt tone ett eneste bånd.
I iii V
<---F---> <---Am---> |<---C--->
|---|---|---|---|---|---|---|---|---|---|
|-C-|---|---|---|-E-|---|---|-G-|---|---|
|---|-A-|---|---|-C-|---|---|---|-E-|---|
|---|---|-F-|---|---|---|-A-|---|---|-C-|
|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|
| 3 5 | 7 9 |
Så la oss flytte E til F i både iii-akkorden Am, og V-akkorden C, og se hva vi får.
I I Csus4
<---F---> <----F---> Fsus2
|---|---|---|---|---|---|---|---|---|---|
|-C-|---|---|---|---|-F-|---|-G-|---|---|
|---|-A-|---|---|-C-|---|---|---|---|-F-|
|---|---|-F-|---|---|---|-A-|---|---|-C-|
|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|
3 5 7 9
Ved å flytte E til F i en C-akkord får vi en Csus4 eller en Fsus2. I sus4-akkorder er tersen - den tonen som avgjør om en akkord er dur (3) eller moll (b3) - flyttet opp til en ren kvint (4). Og omvendt gjelder det for en sus2-akkord at der er tersen flyttet ned til en stor sekund (2). En Csus4 = Fsus2.
Så hva må du flytte for å gjøre om en Csus4 eller Fsus2 til en F. Jo flytter du G-en opp ett bånd, får du en Fm. Flytter du den ett hakk til, så har du en F-durakkord
F-durtreklangens tre inversjoner:
I I I
<---F---> <----F---> <F>
|---|---|---|---|---|---|---|---|---|---|
|-C-|---|---|---|---|-F-|---|---|---|-A-|
|---|-A-|---|---|-C-|---|---|---|---|-F-|
|---|---|-F-|---|---|---|-A-|---|---|-C-|
|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|
3 5 7 9
Dette mønstret gjelder for alle durtreklanger. Flytter du samme mønstret opp to bånd, så finner du en G osv. Det gjelder bare å passe på hva som er grunntonen (1) i hver av inversjonene.
<---G---> <----G---> <G>
|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|-5-|---|---|---|---|-1-|---|---|---|-3-|
|---|---|---|-3-|---|---|-5-|---|---|---|---|-1-|
|---|---|---|---|-1-|---|---|---|-3-|---|---|-5-|
|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|---|---|
3 5 7 9 12
Se CAGED- for å se hvordan du enkelt kan bygger ut inversjonene av durtreklanger til barre-akkorder.
Inversjoner av molltreklanger fra akkordskalaen
For å finne inversjonene til molltreklangen Gm, gjør vi på samme måte. Vi tar annenhver akkord i akkordskalaen.
ii IV vi
<--Gm--> <--Bb---> <---Dm--->
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|-D-|---|---|-F-|---|---|---|-A-|---|---|---|
|---|---|-Bb|---|---|---|-D-|---|---|-F-|---|---|---|
|---|---|---|---|-G-|---|---|-Bb|---|---|---|-D-|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
3 5 7 9 12
Vi gjør først om Hb til Gm som over, ved å flytte F-en til den tonen som mangler, nemlig den neste skalatonen, G. Vi flytter også F til G i akkorden Dm, og får da en Dsus4 = Gsus2
ii ii Dsus4
<--Gm--> <--Gm---> <--Gsus2-->
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|-D-|---|---|---|---|-G-|---|-A-|---|---|---|
|---|---|-Bb|---|---|---|-D-|---|---|---|---|-G-|---|
|---|---|---|---|-G-|---|---|-Bb|---|---|---|-D-|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
3 5 7 9 12
Endelig gjør vi om Dsus4 = Gsus2 til en Gm, ved å flytte den unike tonen A opp til den som mangler fra den forrige, nemlig Hb.
ii ii ii
<--Gm--> <--Gm---> <--Gm-->
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|-D-|---|---|---|---|-G-|---|---|-Bb|---|---|
|---|---|-Bb|---|---|---|-D-|---|---|---|---|-G-|---|
|---|---|---|---|-G-|---|---|-Bb|---|---|---|-D-|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
3 5 7 9 12
Se CAGED- for hvordan du bygger ut barre-akkorder og skalaer fra disse inversjonene.
Durskalaen harmonisert med treklanger:
| Skalatrinn | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| B-durskalaen | B | C#m | D#m | E | F# | G#m | A#dim |
| E-durskalaen | E | F#m | G#m | A | B | C#m | D#dim |
| A-durskalaen | A | Bm | C#m | D | E | F#m | G#dim |
| D-durskalaen | D | Em | F#m | G | A | Bm | C#dim |
| G-durskalaen | G | Am | Bm | C | D | Em | F#dim |
| C-durskalaen | C | Dm | Em | F | G | Am | Bdim |
| F-durskalaen | F | Gm | Am | Bb | C | Dm | Edim |
| Bb-durskalaen | Bb | Cm | Dm | Eb | F | Gm | Adim |
| Eb-durskalaen | Eb | Fm | Gm | Ab | Bb | Cm | Ddim |
| Ab-durskalaen | Ab | Bbm | Cm | Db | Eb | Fm | Gdim |
| Db-durskalaen | Db | Ebm | Fm | Gb | Ab | Bbm | Cdim |
| Gb-durskalaen | Gb | Abm | Bbm | Cb | Db | Ebm | Fdim |
| Harmonisk funksjon | Tonika | supertonika | mediant | subdominant | dominant | submediant | subtonika |
Eksempler på akkorder
<imgcaption skala6| Skalaene B-dur, E-dur, A-dur og D-dur harmonisert med treklanger. Det er her valgt fireklanger på femte og syvende trinn>
 </imgcaption>
</imgcaption>
<imgcaption skala7| Skalaene G-dur, C-dur, F-dur og Bb-dur harmonisert med treklanger. Det er her valgt fireklanger på femte og syvende trinn>
 </imgcaption>
</imgcaption>
<imgcaption skala8| Skalaene Eb-dur, Ab-dur, Db-dur og F#-dur harmonisert med treklanger. Merk fireklanger på femte og syvende trinn>
 </imgcaption>
</imgcaption>
Fortsettelse følger
Harmonisert fireklanger i dur
| Skalatrinn | I | ii | iii | IV | V | vi | vii |
|---|---|---|---|---|---|---|---|
| B-durskalaen | Bmaj7 | C#m7 | D#m7 | Emaj7 | F#7 | G#m7 | A#m7b5 |
| E-durskalaen | Emaj7 | F#m7 | G#m7 | Amaj7 | B7 | C#m7 | D#m7b5 |
| A-durskalaen | Amaj7 | Bm7 | C#m7 | Dmaj7 | E7 | F#m7 | G#m7b5 |
| D-durskalaen | Dmaj7 | Em7 | F#m7 | Gmaj7 | A7 | Bm7 | C#m7b5 |
| G-durskalaen | Gmaj7 | Am7 | Bm7 | Cmaj7 | D7 | Em7 | F#m7b5 |
| C-durskalaen | Cmaj7 | Dm7 | Em7 | Fmaj7 | G7 | Am7 | Bm7b5 |
| F-durskalaen | Fmaj7 | Gm7 | Am7 | Bbmaj7 | C7 | Dm7 | Em7b5 |
| Bb-durskalaen | Bbmaj7 | Cm7 | Dm7 | Ebmaj7 | F7 | Gm7 | Am7b5 |
| Eb-durskalaen | Ebmaj7 | Fm7 | Gm7 | Abmaj7 | Bb7 | Cm7 | Dm7b5 |
| Ab-durskalaen | Abmaj7 | Bbm7 | Cm7 | Dbmaj7 | Eb7 | Fm7 | Gm7b5 |
| Db-durskalaen | Dbmaj7 | Ebm7 | Fm7 | Gbmaj7 | Ab7 | Bbm7 | Cm7b5 |
| Gb-durskalaen | Gbmaj7 | Abm7 | Bbm7 | Cbmaj7 | Db7 | Ebm7 | Fm7b5 |
| Harmonisk funksjon | Tonika | supertonika | mediant | subdominant | dominant | submediant | subtonika |